Here is, as every year, an overview of some of the papers and books I read this year. The main topics are causality, explainability, uncertainty quantification (conformal learning), and data-centric machine learning.

posted at: 10:39 | path: /ML | permanent link to this entry
Here is, as every year, an overview of the papers and books I read this year. The main topics are transformers, graph neural nets, optimization, differentiability and time series.

posted at: 17:32 | path: /ML | permanent link to this entry
As every year, here is a list of what I have read and found interesting this year in machine learning.
Several topics escaped the machine learning world and also appeared in mainstream news: generative models, with Dall-E 2 and stable diffusion, and transformers, with ChatGPT.
Other topics, not in the mainstream news, include graph neural nets, causal inference, interpretable models, and optimization.
If you want a longer reading list:
http://zoonek.free.fr/Ecrits/articles.pdf

posted at: 15:26 | path: /ML | permanent link to this entry
As every year, here are some of the papers I read this year, covering topics such as copulas, convex and non-convex optimization, reinforcement learning, Shapley score, loss landscape, time series with missing data, neural ODEs, graphs, monotonic neural nets, linear algebra, variance matrices, etc.
If you want a shorter reading list:
Reinforcement learning https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3554486 ADMM https://arxiv.org/abs/1909.10233 Copulas https://link.springer.com/book/10.1007/978-3-030-13785-4
If you want a longer list:
http://zoonek.free.fr/Ecrits/articles.pdf

posted at: 11:16 | path: /ML | permanent link to this entry
As every year, here is a list of the papers, books or courses I have found intersting this year: they cover causality, alternatives to backpropagation (DFA, Hebbian learning), neural differential equations, mathematics done by computers, artificial general intelligence (AGI), explainable AI (XAI), fairness, transformers, group actions (equivariant neural networks), disentangled representations, discrete operations, manifolds, topological data analysis, optimal transport, semi-supervised learning, and a few other topics.

posted at: 11:13 | path: /ML | permanent link to this entry
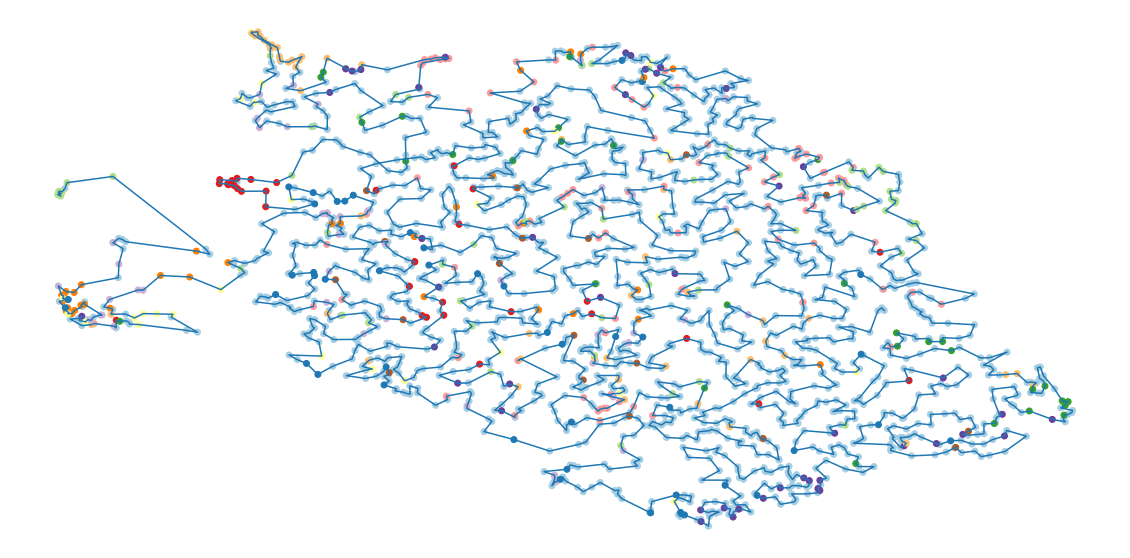
When I have a large pile of papers to read, in electronic form, I do not want to read them in a random order: I prefer to read related papers together.
How can we sort hundreds of papers by topic?
Let us take the example of the CVPR conference (more than 1000 papers). We will proceed as follows:
- Retrieve the abstract of all the papers;
- Compute the embedding of each abstract, using the DistilBert pretrained model, from HuggingFace's Transformers library;
- Reduce the dimension to 2, to plot the data, using UMAP (we could use t-SNE instead);
- Find an ordering of the papers, i.e., a path, minimizing the total distance in the UMAP-reduced space (we could compute the distances in the original space, instead), using ortools's TSP solver.
The result can be a text file with the paper titles, links and abstract, in the order, or a pdf file with the first page of each paper, in the order (you can also read the begining of the introduction, and enjoy the plot on the first page, should there be one).
posted at: 14:47 | path: /ML | permanent link to this entry
Here are some of the topics I found interesting at the recent ICLR 2020 conference.

While most neural networks are based on linear transformations and element-wise nonlinearities, one deceptively simple operation is at the core of many innovations (LSTM, attention, hypernetworks, etc.): multiplication.
The notion of gradient is omnipresent in deep learning, but we can compute several of them (gradient of the output or of the loss, wrt the input or the parameters), and they all have their uses.
There is an increasing interplay between classical algorithms (numeric algorithms, machine learning algorithms, etc.) and deep learning: we can use algorithms as layers inside neural nets, we can use neural nets as building blocks inside algorithms, and we can even put neural nets inside neural nets -- anything in a neural net can be replaced by another neural net: weights, learning rate schedule, activation functions, optimization algorithm, loss, etc.
Our understanding of why deep learning works has improved over the years, but most of the results have only been proved for unrealistic models (such as linear neural nets). Since there was also empirical evidence for more realistic models, it was widely believed that those results remained valid for general networks. That was wrong.
We often consider that the set of possible weights for a given neural net is Euclidean (in particular, flat) -- it is an easy choice, but not a natural one: it is possible to deform this space to make the loss landscape easier to optimize on. The geometry of the input and/or the output may not be Euclidean either: for instance, the orientation of an object in 3D space is a point on a sphere.
Convolutional neural networks look for patterns regardless of their location in the image: they are translation-equivariant. But this is not the only desirable group action: we may also want to detect scale- and rotation-invariant patterns.
Neural networks are notorious for making incorrect predictions with high confidence: ensembles can help detect when this happens -- but there are clever and economical ways of building those ensembles, even from a single model.
Supervised learning needs data. Labeled data. But the quality of those labels is often questionable: we expect some of them to be incorrect, and want our models to account for those noisy labels.
With the rise of the internet of things and mobile devices, we need to reduce the energy consumption and/or the size of our models. This is often done by pruning and quantization, but naively applying those on a trained network is suboptimal: an end-to-end approach works better.
Adversarial attacks, and the ease at which we can fool deep learning models, are frightening, but research on more robust models progresses -- and so does that on attacks to evade thoses defenses: it is still a cat-and-mouse game.
The conference also covered countless other topics: small details to improve the training of neural nets; transformers, their applications to natural language processing, and their generalizations to images or graphs; graph neural networks, their applications to knowledge graphs; compositionality; disentanglement; reinforcement learning; etc.
posted at: 11:33 | path: /ML | permanent link to this entry
I have not attended the NeurIPS conference, but I have spent a few weeks binge-watching most of it. Here are some of the topics I have found interesting.
If you want to read/watch something funny, check the following topics: What happens if you set all the weights of a neural network to the same value? What happens if a layer becomes infinitely wide? What happens if a network becomes infinitely deep? Is it really pointless to consider deep linear networks?
If you want to look at nice pictures, check the recent explorations of the loss surface of neural nets.
If you want something easy to understand, check the discussions on fairness.
If you want something new, check the new types of layers (in particular those corresponding to combinatorial operations), sum-product networks (which are more expressive than traditional neural nets), mesure-valued derivatives (a third way of computing the gradient of an expectation), the many variants of gradient descent, second-order optimization methods, perhaps also Fourier-sparse set functions and the geometric approach to information theory.
If you want applications to finance... there were almost none. There was a workshop on "robust AI for the financial services", but the corresponding talks were either rather empty or only had a thin connection to finance.

posted at: 14:30 | path: /ML | permanent link to this entry